Combo Brewing Fundamentals: Counting Problems
08/30/2024
It's not that hard to find combos in Magic. With how the Internet works, it's pretty common for two- or three- card combos to be found and commented on basically as soon as a card is spoiled. This happened with Nadu - if I recall correctly, there was even a Nadu deck Discord server made before spoiler season had concluded! It's just pretty easy to put combos together when you're thinking theoretically.
The much, much harder part is turning those theoretical card interactions into an actual, functional deck. Combos often seem much better in theory - where you can just imagine drawing and casting the right cards all together - than in practice - where you have to deal with actually finding your combo pieces, and assembling them through possible interaction.
So, today I want to talk about one of the fundamental concepts involved in turning a combo idea into reality - something I like to call the "Counting Problem".
Part 1: One Card Per Turn
The basis of the Counting Problem is simply one of the fundamentals of Magic: by default, every turn you draw one card, and no more.
There are certainly cards you can play to change this - either
cantrips that replace themselves and get you deeper into your deck, or card draw that increases the raw number of cards you have access to. But without these kinds of cards, you're at the mercy of your draw step.You might wonder: how bad can that be, exactly? You start with 7 cards, which is surely plenty! But quite often, you'll find that those 7 cards pretty quickly run out, even when you're getting one per turn. And the main purpose of the Counting Problem is to highlight exactly when those baseline cards are just not enough.
Example: Ygra Combo in Pioneer
The best way to to demonstrate how the Counting Problem applies is through example. So, let's consider a recent (and quite relevant!) combo: Ygra in Pioneer.
Ygra, Eater of All is a new card from Bloomburrow that introduced a new combo into Pioneer: if you have Ygra on the battlefield, one copy of Cauldron Familiar on the battlefield, and another Familiar in your graveyard, you can infinitely loop the two Familiars, repeatedly sacrificing one to bring the other back.
So, in order to combo, we need to put Ygra onto the battlefield, and find two copies of Cauldron Familiar, either by drawing or milling them. How many cards does that take?
Well, naively, we need to be able to cast Ygra. This implies that we need 5 lands in play. And on top of that, we need the 3 combo pieces: one Ygra and two Familiars. So in total, that adds up to 8 cards we need to enact our combo.
How does that line up with the natural cards we draw? Well, presumably we want to combo as quickly as possible - so let's imagine it's turn 5. If we're on the play, then by then we've drawn our opening 7 cards plus 4 draws steps, making that 11 cards in total.
With that framing, needing 8 of those 11 cards to go towards our combo is quite a lot! That only leaves 3 cards left for interaction or alternate threats - which is pretty unacceptable in current Pioneer if you ask me, especially if you're planning to combo as late as turn 5.
This, then, is the first of our Counting Problems: trying to rely on natural draw steps to put the Ygra combo into play leaves very little room for anything else.
11 - 8 = 3
At the same time, we can consider a different kind of Counting Problem as well, and perhaps an even more pressing one - namely: how likely is it, actually, to find all of our combo pieces?
We can turn to a multivariate intersect calculator for that. And, well, the numbers aren't particularly appealing, to say the least:
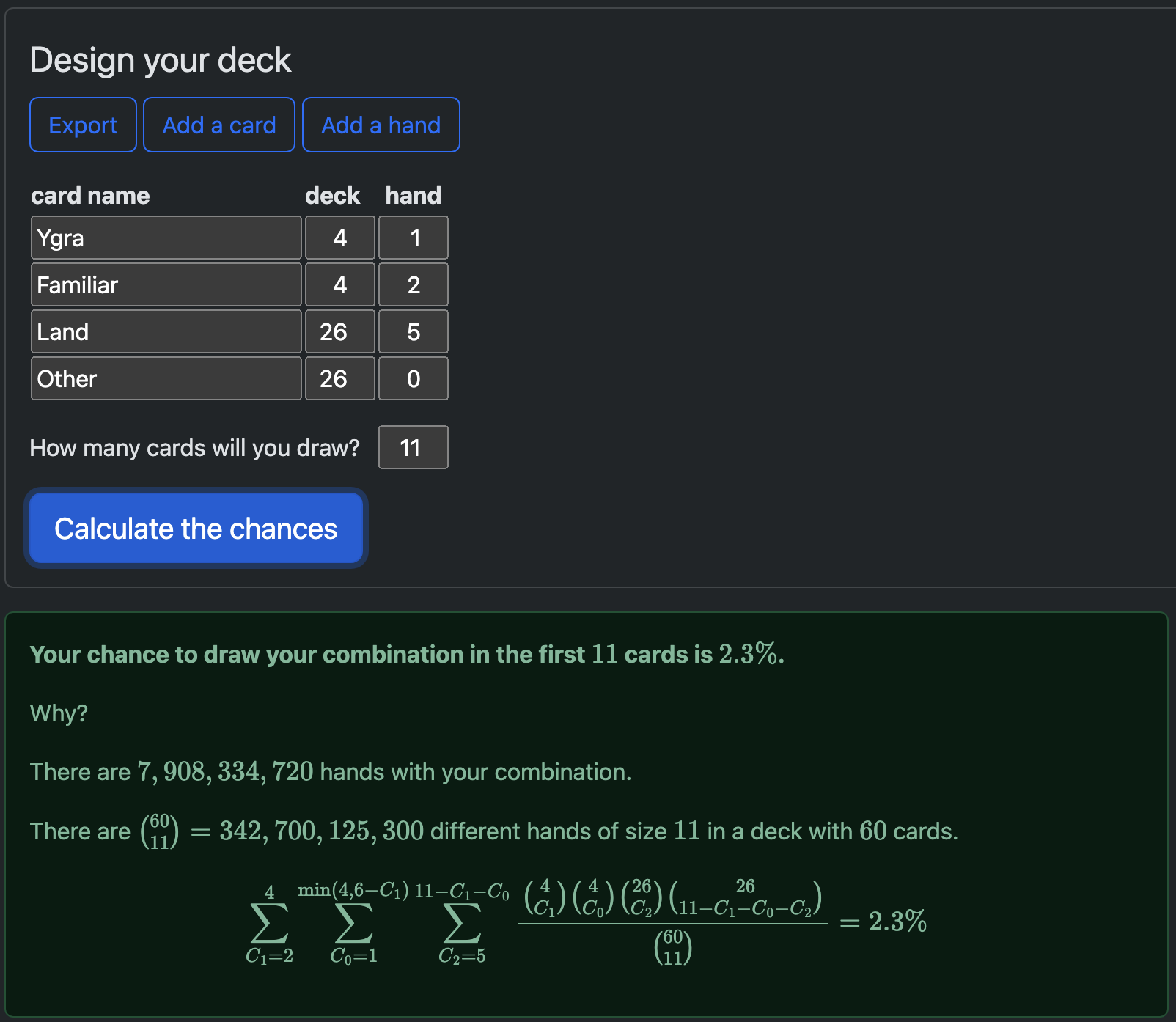
wow, almost 2.5%!
So then, these are the two Counting Problems we face: if we rely purely on natural draw steps to try to assemble our combo, then we won't have very many other cards to work with, and we have a miniscule chance of assembling our combo. Clearly, we must do better.
Part 2: Manipulating the Count
Okay, so now we know we shouldn't rely purely on our natural draw steps to assemble combos. But that much was probably already obvious, even without the math. But then, how do we solve this?
Of course, there's the cantrips and card draw we talked about earlier. Cantrips help purely with finding the combo, by making sure we get to look at more cards. Card draw also helps a bit with finding the combo, but more importantly addresses the raw card count problem, giving us more total material to work with.
But of course, there are many other ways still to improve our counts. Let's once again take a look at some examples with the Ygra deck for inspiration.
Self-Mill
Of course, one of the most obvious ways to improve our count is by milling our Cauldron Familiars instead of drawing and casting them. That's one of the benefits of this combo, after all - two of our pieces can just come from the graveyard! (well, we either need a food or non-Ygra creature in play in that case, but that should be really easy)
This opens up many, many ways to improve our count of cards seen, improving our consistency. There are lots of self-mill cards in Pioneer, after all - from
Stitcher's Supplier to Grisly Salvage to the recently-printed Cache Grab.And if we add enough self-mill cards to our deck, such that we expect to mill one or two copies of Familiar every game, we can at some point even consider that an improvement to our raw card count problems as well! If we can reliably get Familiars from the graveyard, then we won't need to spend cards from our hand on them.
Card Draw and Ramp - Deadly Dispute
One very natural inclination when building Ygra as a deck is to look at previous versions of Pioneer Sacrifice decks - where, notably, Cauldron Familiar has seen play. From this, we can take the card
Deadly Dispute, which makes a lot of sense in a deck with Familiars and food ripe for sacrificing!And as it turns out, Deadly Dispute actually helps a lot with the raw cards Counting Problem we're facing. Assuming we can minimize the additional cost of sacrificing something to near-zero, it actually contributes +2 to our card count for combo purposes!
Spending one card to draw two cards is naturally going +1 on literal card count. But in this case, the treasure can also easily be considered to be +1 card. One of the issues we had with Ygra is that it simply cost 5 mana. So if we want to naturally cast Ygra, it takes five whole other cards (lands) in order to do so! But since we're unlikely to want to play other 5s in our deck, we can pretty easily count the treasure we get from Deadly Dispute as a substitue for the 5th land - letting Dispute contribute a full +2.
Sidenote: The Costs of a High Curve
This concept of a Counting Problem really highlights how a 6 mana card costs so much more than just twice a 3 mana card. Every successive land drop is harder to make, as you draw fewer than one land per turn on average. Continuing to make land drops past a certain point starts eating into the other resources you have at your disposal, and often requires active effort invested into generating card advantage to be able to continue to fuel making more land drops while casting more spells.
In fact, despite my focus on how Counting Problems affect combo decks, the concept is not limited to unfair strategies! It's simply easier to talk about such a discrete criteria when we're working within the highly defined bounds of a combo - where a certain set of conditions will cause us to win the game, and a large part of our gameplan is focused on that.
But we can apply similar concepts to fair decks - this is why control decks often play divinations, for example, as they really want to hit their land drops even late into the game. And this is why you shouldn't just stick many 6-drops into any random deck with no support - you actually need some amount of dedicated resources to make sure that you can meaningfully cast that 6 drop without giving up too much in other respects.
Incidentally, this is why cards like
Big Score and Unexpected Windfall have seen play at various points in Magic's history. These are cards that, while somewhat expensive and inefficient, are in fact powerful tools at solving Counting Problems! Not only do they filter through cards, digging for what you need; they also provide two treasures that let you cast a more expensive spell without dedicating more involved deck architecture to hitting land drops.Card Draw Engines - Trail of Crumbs
As we look at how Cauldron Familiar decks have been built in the past, we might also come across the card
Trail of Crumbs.This card is, of course, a potent card draw engine with the likes of
Cauldron Familiar and Witch's Oven. But one of the problems with it is that it is quite slow.Let's say we want to assemble our combo on turn 5. By then, we'll presumably have 15 mana total that we can spend - 1 on turn 1, 2 on turn 2, etc. If we assume we're casting Ygra on turn 5 to start the combo, then that's 5 of that 15 mana spent. And then if we want to make Trail of Crumbs contribute more than +1 to our card count, we need it to draw 3 cards - which means at least 5 mana spent on casting and paying for it. That then leaves only 5 other mana to work with, and that's assuming we were perfectly efficient every turn!
This is, in some sense, another kind of Counting Problem - the mana just doesn't really make sense for trying to trigger Trail of Crumbs three times in the first five turns. But mana Counting Problems are a bit different than those involving cards seen or cards drawn - namely, they very quickly get solved by simply waiting a couple more turns. While you only draw one card per turn naturally, you generally make much more than one mana per turn.
For instance, if we instead decide we're probably not comboing until turn 6, then we potentially have access to a full 6 more mana, for up to 21 total! So, while Trail of Crumbs might be a bad fit for fixing card-related Counting Problems before turn 6, it could be a valuable part of a gameplan that instead looks to combo later into the game, rather than turboing it out.
Flipping the Script - Scavenger's Talent
Finally, one of the best ways to solve a Counting Problem is simply to attack the problem from a completely different angle. And that's exactly what
Scavenger's Talent does.First of all, it passively provides some food to fuel the various other parts of your sacrifice deck. This isn't all that necessary to the combo, but it's a nice tool to have. It helps the card not quite cost a full card, which is nice.
Secondly, by itself it serves as a lot of self-mill. If you're doing the cat oven combo, a level 2 Talent will mill 4 cards a turn! This lets you find your combo pieces very quickly. This is a card that can solve our cards-looked-at Counting Problem on its own.
Finally, and perhaps most importantly, it serves as an extremely card-efficient way to both find Ygra and put it into play! Instead of requiring 5 lands to cast Ygra, we can now have as few as the 3 necessary to level up Talent. And while you're never going to be able to reanimate Ygra on turn 3, this still means that you just don't need your 4th and 5th lands to combo, which is huge.
And on top of all that, Talent quite nicely provides the self-mill to dig for the Ygra, as well as the extra material to sacrifice to level 3 to get back Ygra. And once you do reanimate Ygra, you even get three additional mill triggers to dig 6 more cards for Familiars. It's just a perfect, self-contained package, that really changes the dynamics of the combo!
By turn 3, we'll have drawn 9 cards naturally, and only really need to use 4 of those for the combo, leaving 5 cards to interact or enact other gameplans with! Of course, it won't always work out like this, and we won't always have Talent, but the fact that we can minimize our combo requirements this much is huge!
Re-evaluating The Count
So, now with all of these tools, where do we stand on these Counting Problems?
Well, our minimal combo package is now simply one copy of Scavenger's Talent and three lands! Of course, we also need some way to trigger the Scavenger's Talent - perhaps some of the other cards in our hand will involve sacrificing various kinds of permanents - but we can theoretically dedicate as few as 4 cards out of the ones we draw to the combo! This is a drastic improvement, and lets us interact and play a normal game much more often.
How about the other Counting Problem? Well, as long as we get our Scavenger's Talent setup, we should have no trouble milling dozens of cards per game, so it should be pretty easy to rely on that too.
But of course, things aren't quite that simple. All of these calculations depend on drawing a Scavenger's Talent - and that's by no means a guarantee! So we probably still want to build in some resiliency into the deck, perhaps by adding cards like
Deadly Dispute to be able to reasonably count to the combo when we don't have Talent; or perhaps by playing cantrips like Cache Grab in order to find Scavenger's Talent more often.The important takeaway, though, is how pivotal Scavenger's Talent is in solving the deck's problems. We needed quite a bit more than simply taking normal draw steps to be able to count to enough cards to assemble the combo. And while there are many tools we could employ to up our card counts, the most effective method by far is refocusing the deck around Scavenger's Talent.
Part 3: Other Counting Examples
To solidify this concept, let's quickly go over a few more examples of combo decks, and talk about how they deal with Counting Problems.
Banned Counting Efficiency: Amalia and Nadu
The most recent banlist saw two combo decks banned from their respective formats:
Amalia Benavides Aguirre and Nadu, Winged Wisdom.Of course, the reason for these bans were somewhat complex - both cards also led to terrible play patterns and unhealthy effects on the format - but at the end of the day, a big part of why the cards were banned was that the combos they were part of were simply too strong.
And you can actually get a sense from this from simply looking at their card counts: Amalia can kill as early as turn 3 with simply 3 lands, Amalia,
Wildgrowth Walker, and a way to gain life or explore (6 cards total). Nadu can kill as early as turn 3 with 3 lands, Nadu, and Shuko (5 cards total) - and one of the lands can even double as the Shuko if it's a turn 1 Urza's Saga!The sheer minimality of these two deck's combos lets both of them devote the entire rest of their deck to protection and redundancy. Amalia can run out the combo on turn 3, with three more ways in hand to get back or find more combo pieces if interacted with. Nadu can do even better, as many ways of interacting with Nadu trigger it and draw its controller even more cards.
Lotus Field: Barely Enough for Grazer
Pioneer Lotus Field as a deck generally functions by putting
Lotus Field into play, copying it with Thespian's Stage, and then using untapping rituals like Hidden Strings, Vizier of Tumbling Sands, and Pore Over the Pages to generate enough mana to cast Emergent Ultimatum.There are many different lines that the deck can employ, but the most common lines require playing Lotus, Stage, and enough rituals to get to 8-ish mana to win with Emergent Ultimatum. This then requires 4 lands total (two lands to start, then Lotus, then Stage), 1 copy of Ultimatum, and 1-2 rituals.
In addition to that, speed is a concern - Lotus Field decks are often built to try and win around turn 3 or 4 when they're not disrupted. But this requires more resources - you often need more like 2-3 rituals to win on turn 4, and a copy of
Arboreal Grazer if you want to win on turn 3.And it turns out the numbers are pretty tight here - 2 lands + 1 Lotus + 1 Stage + 1 Grazer + 2 Rituals + 1 Ultimatum is 8 cards out of the 9 you naturally have access to on the play! Thankfully, Vizier and Pore help here, as they are small rituals that replace themself or even go up cards, respectfully. But even still, we can see how maximizing speed is fairly card-intensive.
At the same time, these are also a lot of separate specific cards we need to find. So, it can be pretty hard to assemble the combo without help - and this is why Lotus combo generally plays cards like
Impulse, Temple of Mystery, and of course Sylvan Scrying.Thankfully, we can afford to dedicate so much deck space to speed and consistency, because the nice thing about Lotus is that it's extremely hard to interact with! Not much in the format can remove a hexproof land from the battlefield, and beyond that the only possible interaction comes from discard spells and countermagic. So, instead of building a more resilient gameplan, it is quite standard to simply go all-in.
Early Access Otter Storm Doesn't Work
During Bloomburrow Early Access, I played a very janky very bad combo deck that involved using a
Twinferno'd Beseech the Mirror to storm off with Stormsplitter. I don't want to explain the full combo line, as the deck is quite bad and the exact details aren't that relevant - I'll leave that as an exercise for the reader :P
the Otter Storm deck in question
But the short version is: in order to pull off the combo you needed to cast Twinferno to copy your bargained Beseech, and you needed not just one but two bargain fodder to be in play (as later down the line you need to pay the bargain cost for another Beseech). So, in total, this adds up to 8 real cards, plus two bargain fodder (which very much aren't free!)
We can pretty quickly see the Counting Problem here - by turn 6, we've only seen 12 cards on the play, and even without counting the bargain fodder required we only have 4 remaining cards to work with! And for a combo that goes off on turn 6, that's just not nearly enough to interact enough to stay alive.
Of course, we have some amount of ways to generate more cards here -
Collector's Vault, for example, helps a lot; and we have plenty of ways to make bargain fodder. But because the mana of 1BBB is so restricting, it's hard to play more than two colors, so the tools we have access to are extremely minimal.So, by its nature, this deck is already fighting an uphill battle to combo. Add to that the fact that it has to play a bunch of combo cards that are pretty bad to draw naturally, and it becomes quite untenable.
Conclusion
The Counting Problem is, at its core, a fairly simple analysis. It merely asks the question: how many cards are you expecting to see / have access to by the time you're trying to enact your main gameplan, and how does that line up with the requirements of that gameplan?
Despite its simplicity, though, it's still a very useful tool for figuring out how to build a resilient gameplan for your deck. A simple analysis, as it turns out, is a great way to get at the fundamentals of how a deck functions.
So, the next time you have a combo idea, try putting it through the simple test of counting.
#FreePalestine | Consider donating to UNWRA or PCRF, supporting protesters locally, and educating yourself.
